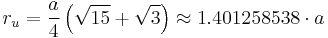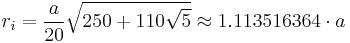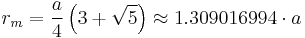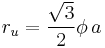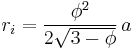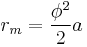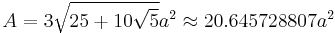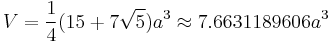Dodecahedron
| Regular Dodecahedron | |
|---|---|
(Click here for rotating model) |
|
| Type | Platonic solid |
| Elements | F = 12, E = 30 V = 20 (χ = 2) |
| Faces by sides | 12{5} |
| Schläfli symbol | {5,3} |
| Wythoff symbol | 3 | 2 5 |
| Coxeter-Dynkin | |
| Symmetry | Ih, [5,3], (*532) |
| References | U23, C26, W5 |
| Properties | Regular convex |
| Dihedral angle | 116.56505° = arccos(-1/√5) |
5.5.5 (Vertex figure) |
Icosahedron (dual polyhedron) |
Net |
|
In geometry, a dodecahedron (Greek δωδεκάεδρον, from δώδεκα 'twelve' + ἕδρα 'base', 'seat' or 'face') is any polyhedron with twelve flat faces, but usually a regular dodecahedron is meant: a Platonic solid. It is composed of 12 regular pentagonal faces, with three meeting at each vertex, and is represented by the Schläfli symbol {5,3}. It has 20 vertices and 30 edges. Its dual polyhedron is the icosahedron, with Schläfli symbol {3,5}.
A large number of other (nonregular) polyhedra also have 12 sides, but are given other names. Other dodecahedrons include the hexagonal bipyramid and the rhombic dodecahedron.
Contents |
Dimensions
If the edge length of a regular dodecahedron is a, the radius of a circumscribed sphere (one that touches the dodecahedron at all vertices) is
and the radius of an inscribed sphere (tangent to each of the dodecahedron's faces) is
while the midradius, which touches the middle of each edge, is
These quantities may also be expressed as
where 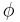 is the golden ratio.
is the golden ratio.
Note that, given a regular pentagonal dodecahedron of edge length one, 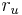 is the radius of a circumscribing sphere about a cube of edge length
is the radius of a circumscribing sphere about a cube of edge length 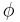 , and
, and 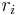 is the apothem of a regular pentagon of edge length
is the apothem of a regular pentagon of edge length 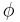 .
.
Area and volume
The surface area A and the volume V of a regular dodecahedron of edge length a are:
Cartesian coordinates
The following Cartesian coordinates define the vertices of a dodecahedron centered at the origin:[1]
- (±1, ±1, ±1)
- (0, ±1/φ, ±φ)
- (±1/φ, ±φ, 0)
- (±φ, 0, ±1/φ)
where φ = (1+√5)/2 is the golden ratio (also written τ) = ~1.618. The edge length is 2/φ = √5–1. The containing sphere has a radius of √3.
Properties
- The dihedral angle of a dodecahedron is 2 arctan(φ) or approximately 116.5650512 degrees.
- If the original dodecahedron has edge length 1, its dual icosahedron has edge length
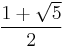 , the golden ratio.
, the golden ratio. - If we build the five Platonic solids with same volume, the dodecahedron has the shortest edges.
- It has 43,380 nets.
- The map-coloring number of a regular dodecahedron's faces is 4.
- The distance between the vertices on the same face not connected by an edge is φ.
Geometric relations
The regular dodecahedron is the third in an infinite set of truncated trapezohedra which can be constructed by truncating the two axial vertices of a pentagonal trapezohedron.
The stellations of the dodecahedron make up three of the four Kepler-Poinsot polyhedra.
A rectified dodecahedron forms an icosidodecahedron.
The regular dodecahedron has 120 symmetries, forming the group 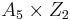 .
.
Icosahedron vs dodecahedron
When a dodecahedron is inscribed in a sphere, it occupies more of the sphere's volume (66.49%) than an icosahedron inscribed in the same sphere (60.54%).
A regular dodecahedron with edge length 1 has more than three and a half times the volume of an icosahedron with the same length edges (7.663... compared with 2.181...).
A Regular Dodecahedron has fewer faces than the icosahedron, but more vertices.
Related polyhedra
The dodecahedron can be transformed by a truncation sequence into its dual, the icosahedron:
| Picture | Dodecahedron |
Truncated dodecahedron |
Icosidodecahedron |
Truncated icosahedron |
Icosahedron |
|---|---|---|---|---|---|
| Coxeter-Dynkin |
The regular dodecahedron is a member of a sequence of otherwise non-uniform polyhedra and tilings, composed of pentagons with face configurations (V3.3.3.3.n). (For n>6, the sequence consists of tilings of the hyperbolic plane.) These face-transitive figures have (n32) rotational symmetry.
V3.3.3.3.3 (332) and (532) |
V3.3.3.3.4 (432) |
V3.3.3.3.5 (532) |
V3.3.3.3.6 (632) |
V3.3.3.3.7 (732) |
Vertex arrangement
The dodecahedron shares its vertex arrangement with four nonconvex uniform polyhedra and three uniform polyhedron compounds.
Five cubes fit within, with their edges as diagonals of the dodecahedron's faces, and together these make up the regular polyhedral compound of five cubes. Since two tetrahedra can fit on alternate cube vertices, five and ten tetrahedra can also fit in a dodecahedron.
Stellations
The 3 stellations of the dodecahedron are all regular (nonconvex) polyhedra: (Kepler-Poinsot polyhedra)
| 0 | 1 | 2 | 3 | |
|---|---|---|---|---|
| Stellation | Dodecahedron |
Small stellated dodecahedron |
Great dodecahedron |
Great stellated dodecahedron |
| Facet diagram |
Other dodecahedra
The truncated pentagonal trapezohedron has d5d dihedral symmetry. |
The pyritohedron has th tetrahedral symmetry. |
The term dodecahedron is also used for other polyhedra with twelve faces, most notably the rhombic dodecahedron which is dual to the cuboctahedron (an Archimedean solid) and occurs in nature as a crystal form.[2] The Platonic solid dodecahedron can be called a pentagonal dodecahedron or a regular dodecahedron to distinguish it. The pyritohedron is an irregular pentagonal dodecahedron.
Other topologically distinct dodecahedra include:
- Uniform polyhedra:
- Pentagonal antiprism – 10 equilateral triangles, 2 pentagons
- Decagonal prism – 10 squares, 2 decagons
- Johnson solids (regular faced):
- Pentagonal cupola – 5 triangles, 5 squares, 1 pentagon, 1 decagon
- Snub disphenoid – 12 triangles
- Elongated square dipyramid – 8 triangles and 4 squares
- Metabidiminished icosahedron – 10 triangles and 2 pentagons
- Congruent nonregular faced: (face-transitive)
- Hexagonal bipyramid – 12 isosceles triangles, dual of hexagonal prism
- Hexagonal trapezohedron – 12 kites, dual of hexagonal antiprism
- Triakis tetrahedron – 12 isosceles triangles, dual of truncated tetrahedron
- Rhombic dodecahedron (mentioned above) – 12 rhombi, dual of cuboctahedron
- Other nonregular faced:
- Hendecagonal pyramid – 11 isosceles triangles and 1 hendecagon
- Trapezo-rhombic dodecahedron – 6 rhombi, 6 trapezoids – dual of Triangular orthobicupola
- Rhombo-hexagonal dodecahedron or Elongated Dodecahedron – 8 rhombi and 4 equilateral hexagons.
In all there are 6,384,634 topologically distinct dodecahedra.[3]
History and uses
Dodecahedral objects have found some practical applications, and have also played a role in the visual arts and in philosophy.
Plato's dialogue Timaeus (c. 360 B.C.) associates the other four platonic solids with the four classical elements, adding that "there is a fifth figure (which is made out of twelve pentagons), the dodecahedron—this God used as a model for the twelvefold division of the Zodiac."[4] Aristotle postulated that the heavens were made of a fifth element, aithêr (aether in Latin, ether in American English), but he had no interest in matching it with Plato's fifth solid.
A few centuries later, small, hollow bronze Roman dodecahedra were made and have been found in various Roman ruins in Europe. Their purpose is not certain.
In twentieth century art, dodecahedra appear in the work of M. C. Escher, such as his lithograph Reptiles (1943), and in his Gravitation. In Salvador Dalí's painting The Sacrament of the Last Supper (1955), the room is a hollow dodecahedron.
In modern role-playing games, the dodecahedron is often used as a twelve-sided die, one of the more common polyhedral dice. Some quasicrystals have dodecahedral shape (see figure). Some regular crystals such as garnet and diamond are also said to exhibit "dodecahedral" habit, but this statement actually refers to the rhombic dodecahedron shape.[2]
The popular puzzle game Megaminx is in the shape of a dodecahedron.
In the children's novel The Phantom Tollbooth, the Dodecahedron appears as a character in the land of Mathematics. Each of his faces wears a different expression – e.g. happy, angry, sad – which he swivels to the front as required to match his mood.
Shape of the Universe
Various models have been proposed for the global geometry of the universe. In addition to the primitive geometries, these proposals include the Poincaré dodecahedral space, a positively curved space consisting of a dodecahedron whose opposite faces correspond (with a small twist). This was proposed by Jean-Pierre Luminet and colleagues in 2003[5][6] and an optimal orientation on the sky for the model was estimated in 2008.[7]
As a graph
The skeleton of the dodecahedron – the vertices and edges – form a graph. The high degree of symmetry of the polygon is replicated in the properties of this graph, which is distance-transitive, distance-regular, and symmetric. The automorphism group has order 120. The vertices can be colored with 3 colors, as can the edges, and the diameter is 5.[8]
The dodecahedral graph is Hamiltonian – there is a cycle containing all the vertices. Indeed, this name derives from a mathematical game invented in 1857 by William Rowan Hamilton, the icosian game. The game's object was to find a Hamiltonian cycle along the edges of a dodecahedron.
See also
- Spinning dodecahedron
- Truncated dodecahedron
- Snub dodecahedron
- Pentakis dodecahedron
- 120-cell: a regular polychoron (4D polytope) whose surface consists of 120 dodecahedral cells.
References
- ^ Weisstein, Eric W., "Icosahedral group" from MathWorld.
- ^ a b Dodecahedral Crystal Habit
- ^ Counting Polyhedra – Numericana
- ^ Plato, Timaeus, Jowett translation.
- ^ "Is the universe a dodecahedron?", article at PhysicsWeb.
- ^ Luminet, Jean-Pierre; Jeff Weeks, Alain Riazuelo, Roland Lehoucq, Jean-Phillipe Uzan (2003-10-09). "Dodecahedral space topology as an explanation for weak wide-angle temperature correlations in the cosmic microwave background". Nature 425 (6958): 593–5. arXiv:astro-ph/0310253. Bibcode 2003Natur.425..593L. doi:10.1038/nature01944. PMID 14534579.
- ^ Roukema, Boudewijn; Zbigniew Buliński, Agnieszka Szaniewska, Nicolas E. Gaudin (2008). "A test of the Poincaré dodecahedral space topology hypothesis with the WMAP CMB data". Astronomy and Astrophysics 482 (3): 747. arXiv:0801.0006. Bibcode 2008A&A...482..747L. doi:10.1051/0004-6361:20078777.
- ^ Weisstein, Eric W., "Dodecahedral Graph" from MathWorld.
External links
- Weisstein, Eric W., "Dodecahedron" from MathWorld.
- Weisstein, Eric W., "Elongated Dodecahedron" from MathWorld.
- Richard Klitzing, 3D convex uniform polyhedra, o3o5x – doe
- Editable printable net of a dodecahedron with interactive 3D view
- The Uniform Polyhedra
- Origami Polyhedra – Models made with Modular Origami
- Dodecahedron – 3-d model that works in your browser
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra
- VRML models
- Regular dodecahedron regular
- Rhombic dodecahedron quasiregular
- Decagonal prism vertex-transitive
- Pentagonal antiprism vertex-transitive
- Hexagonal dipyramid face-transitive
- Triakis tetrahedron face-transitive
- hexagonal trapezohedron face-transitive
- Pentagonal cupola regular faces
- K.J.M. MacLean, A Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra
- Dodecahedron 3D Visualization
|
|
|||||
|
||||||||||||||||||||||||||